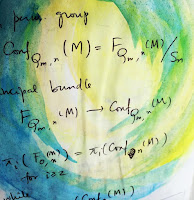When you approach the age of ninety, death does not come unexpectedly: it is the silent shadow that walks with you, that you get to know intimately long before the final encounter. Such is the nature of things, but much as we all know it, friendship remains entirely oblivious of these considerations: when we mourn the loss of a friend our grief does not care whether it is something we logically should have come to expect. I am not going to write here the obituary you all have seen already, the one everybody rushed to publish, from the New York Times (that by their own admission had it ready since 2015) and the BBC, to the various science academies he once presided and the prestigious British universities he had been a faculty member of. I will not give you the Homeric catalog of the ships, with listings of scientific achievements, prizes, and famous theorems. If you want visions of mathematical heroism, there's a whole seven volumes of them: get hold of your library copy of his collected works, open a random page of a random volume and start reading. You will find beauty and poetry in mathematical form.
The idea of beauty as a guiding light, the polar star of the mathematical navigators is not new: after all mathematics and aesthetic beauty have been closely connected since at least the classical canon of the Greeks. This is however one of the most striking manifestations of the principle on such a large scale and within the development of contemporary mathematics. Even when the work is at its most demanding technical depth, it maintains always a sense of elegance, of flowing smoothly (even if not at all easily) along a path of minimal resistance through the landscape of our aesthetic appreciation. To those who wonder whether mathematics should be regarded as a science or as a form of art, this lends enough material for reflection: it is, I guess, both and maybe at the same time neither. Much has been said over the years about how mathematics and theoretical physics grew apart during the twentieth century and then began to come to terms with each other again and find novel forms of convergence at a much more sophisticated level than ever happened before. Atiyah himself played a pivotal role in making this newly rediscovered phase of mutual interaction possible, first with his mathematical development of gauge theories, then by throwing his strenuous support behind the ongoing development of string theory. He was always attentive to many other areas of mathematics where interaction with theoretical physics happened in interesting ways. I became a theoretical physicist first and later a mathematician. I remember the very first research paper I ever read in my early days as a physics student was the Atiyah-Drinfeld-Hitchin-Manin construction of instantons: I was very fortunate to become later on a very good friend and collaborator with two of the authors of that paper.
There is something elusive about the idea of beauty as a guiding principle of mathematical research, something mysterious. After all, let's admit it, most of the time we struggle when we are trying to get things to work, and there does not seem to be much beauty and calm aesthetic appreciation there. We all agree that beauty is truth, truth beauty in front of a Grecian urn, but what about in front of that calculation that still does not come out right? The key here, the very special skill that makes this possible, is to be able to see beyond, to have a larger and deeper horizon, to be able to see the large scale structure before the detail, without implying that the detail will be of lesser importance in the process: "a great mathematical theory should be beautiful on both large and small scales." The idea that there should be a polar star, our sense of beauty and elegance, driving the process of mathematical creativity is closely related to the sense that the origin of mathematical ideas is very far remote from their ultimate polished form that we see as the end result of the process: "People think mathematics begin when you write down a theorem followed by a proof. That's not the beginning, that's the end. ... You are trying to create, just like a musician is trying to create music, or a poet. There are no rules laid down." Trusting this initial vague intuition enough, regardless of its shapeless form, on the guidance of aesthetic feelings alone, to develop it slowly and over time into a solid and profound piece of work is the most remarkable but unfortunately least documented part of mathematical invention: "the crazy part of mathematics is when an idea appears in your head... it floats around in the sky; you look at it and admire its colours. It's just there." It's good to keep in mind that this is how all of it, all of this huge edifice of work, actually happened to take shape. I remember when a then MIT now Harvard professor commented to me on how Atiyah had a special talent for making his papers walk into the history of mathematics: he didn't mean it as a compliment, but in fact it really is. His papers did walk triumphantly into the history of mathematics because he was every so often able to just see the right openings where a new idea would fit perfectly like the key that unlocked the passage door, that opened up a whole new direction, and ended up becoming extremely influential in all the later developments of the field. This is mathematical creativity at its best.
He argued many times against sectarian divides and ferocious territoriality in mathematics: "I dislike frontiers, political and intellectual, and I find that ignoring them is an essential catalyst for creative thought." Some have rightly cared to also mention in their eulogies his genuine desire to build a better and more inclusive mathematical community, his attentiveness to the many overt and hidden forms of discrimination within the mathematical world and in the larger society, his friendliness, approachability and good humour. I am not here to talk about the many human qualities I have come to know and appreciate over these last few years of discussions, friendship, and collaboration. I am not here to weave a golden tapestry with beautiful stories of mathematics and theoretical physics and the thick interplay between geometry and physics that he came to uncover. I am also not here to compile a long and complicated biography.
My purpose here is different. I will momentarily wear the mantle and sandals of Shakespeare's Mark Antony and walk so disguised onto the imaginary stage of a mathematical community I have come over the years to regard as violent and hostile. I am here to deliver that speech this community should not be allowed to eschew on this occasion.
I come to bury Caesar, not to praise him
he was my friend, faithful and just to me
you all did love him once, not without cause
what cause withholds you then, to mourn for him?
Even if now you are all conveniently pretending to forget, many of you, my fellow countrymen of the mathematical Rome, have been the ones that in the past few months have been throwing around a lot of contemptuous unrequested commentaries: your condescension, your scornful rejection were palpably everywhere, but now, oh now you are all praise and pleasant niceties.
For Brutus is an honourable man
so are they all, all honourable men
The mathematicians, all honourable men. Yes, so are they all, all honourable men. Some recent sketched out proofs of famous statements seemed unsound? I am not contesting that. So do not hide behind it, for this is not what I am here to discuss. All the Brutus and Cassius are fully right about it, and besides, they are all honourable men. So please don't hide your daggers behind a mathematical exegesis of this or that text: that will not do.
I speak not to disprove what Brutus spoke,
but here I am to speak what I do know
What is a mathematical idea and how does it form? Let me return for a moment to those quotes I mentioned earlier: ideas are crazy and float around in the sky, they have colour more than substance, a theorem is the end not the beginning. These are really not quite metaphorical statements: that was truly how Michael's superb mathematical mind had always worked. The crazy idea that floats in the sky is the part that you don't normally get to see: you get to see the beautiful fully polished theorem that comes much later at the end of the road. The craziness has all but disappeared, leaving behind just a trace of bewilderment that leaves you wondering, in front of the beautiful finished product, how it all came about. "In the broad light of day mathematicians check their equations and their proofs, leaving no stone unturned in their search for rigour. But at night, under the full moon, they dream, they float among the stars... without dreams there is no art, no mathematics, no life."
What happened then? What happens when the night dream suddenly intrudes upon our daylight reality? I've heard several comments in these months attempting to defend the public circulation (without the author's consent) and public discussion of writings that were meant for the eyes of a small number of acquaintances. Who treated confidentiality so lightly I do not know. It seems there is a growing part of us who would like to publicly police (and play at voting up and down) even our most intimate and ill-formed mathematical ideas. Your voyeuristic mathematical surveillance panopticon will only have the effect to kill all thoughts. We need the night, the full moon, and the floating among the starts. We need to be able to form ideas that are wild and inconclusive and only much later, by the light of day, discard them, after we have entertained them long enough to learn from them: we learn from those ideas that do not work, not just from those that do. We need to be able to trust those we confide in during this early phase to at least attempt to see through what at this stage will literally not stand, while we try to sort it through. It's a delicate process that sometimes collapses and sometimes takes off. That's mathematics, the way it works.
The mathematical community as we know it will love its older members, but only when they quietly disappear. Sure, it would like to see them paraded around at special events, to tell a story or two, but ageism is brutal and extreme, and practiced with a vengeance. To continue to be just what one is, a mathematician, is an act of extreme ambition and defiance in the face of this brutality.
so let it be with Caesar. The noble Brutus
hath told you Caesar was ambitious:
if this were so, it was a grievous fault,
and grievously hath Caesar answer'd it.
Michael was a very social person, which is somewhat rare among mathematicians. Being naturally social has advantages in a healthy surrounding community, but if the community is dysfunctional and toxic, it leaves one more exposed, more easily vulnerable to stab wounds. He complained many times over the years about the virulent ageism of the mathematical community. Very recently, during our last long conversation, he told me he was feeling like a prisoner in a community he had for a long time loved, his access to venues to share and discuss his mathematical dreams and visions progressively shrinking. He had been relying mostly, he said that time, on sharing his thoughts privately with friends. But friends unfortunately are a rare commodity and privacy a much violated terrain.
It is not meet you know how Caesar loved you
But why the urgency, you'll ask, why the rush to share, with the few or the many, ideas not fully formed, why not attend to that same slow process of distillation that leads from this to well grounded and polished final forms we are used to seeing? The continuous speeding up of subjective time is a well known psychological phenomenon we experience throughout the course of our lives. It reaches a frenzied peak at some point, with a compelling sense of time running out in an all consuming rush. Those of you who have close friends in this age range will certainly have experienced, even at a distance, the mounting pressure of this enormous acceleration. Quite unlike the slow-down that common prejudice imagines, life ends in an ultraviolet conflagration of exploding acceleration.
In an interview some years ago he jokingly said "people will say, alright he was a good mathematician, but at the end of his life he lost his marbles". And surely you did say that: you said whatever was easy to say, regardless of its factual reality. That's always the way prejudice works: it replaces a complex reality with a fictional simplicity. For your information, there was no "age problem", not in the sense of all your tasteless and malicious "jokes" and innuendos about cognitive decline. Some bipolar states, yes, which you would not have even attempted to understand, so steeped you all are in your primordial broth of prejudices, so well adapted to its festering ecosystem.
There were those sudden bursts of cosmic energy, the rapid flow of communications sent in the middle of the British night, piling up lots of thoughts and ideas as if the normal linear ordering of time and language would be too poor a medium to convey all that precipitous blossoming: another polar star that often shines too bright. The somber times were mostly silent, though with time I came to understand that a friend's presence was appreciated even then. I miss all of those times, both the highs and the lows: they were not always the best of times for mathematical discussions (but then perhaps sometimes they were) but they were always special and meaningful.
What is it? You'd rather not hear about this? Then put those seven volumes back on the library shelf at once and disappear, because I am sorry my honourable dude, please get it: you cannot have one without the other! Perhaps one day in a future world we will have mathematics without mathematicians, with theorems created by intelligent machines; perhaps they will then be able to generate mathematical beauty without the frightening heights and the depressive lows of human creativity. I doubt it, but at least as long as the highest peaks of mathematical beauty are an exclusive product of the human mind, we must learn to accept the package they come with in its entirety, and learn to appreciate all of it, even the parts that feel uncomfortable to your average well-to-do mathematician.
I should do Brutus wrong, and Cassius wrong,
who, you all know, are honourable men
Was his also an attempt to provoke the community and force it to confront some of these deeds? He did imply that much at times, but I don't think it could have worked: it'd be like trying to shake a rooting hog out of a pit of sludge. Not even this real drama of pain and death will move those very honourable men out of their dull complacency and their respectable brutality. I've heard those among you who came to me and said: tell him that he should stop making claims, whereby you really meant he should stop living. He did, but I am alive, and I remember all of you: don't think that I will not, just because you're now trying to hide your daggers.
During my visits to Edinburgh I had long discussions, both with Michael himself and with his good and generous colleague Andrew, not just about the mathematics, but on the handling of the difficult highs and lows of mathematical creativity, as well as on the hostility of a community that is all too eager to reap the benefits of this process while refusing to acknowledge its functioning and the human cost that comes with it. Over the years Andrew, who understood very well the situation, always found considerate but significant ways to be of help, until he passed away a year ago: another loss of a rare caring and gentle soul in our community. I wish Andrew were still alive today: he would have been able to find a more delicate way of saying what I am now saying. It was in Andrew's nature to be a kind and loving person. I am not, and besides, I am Shakespeare's Mark Antony right now.
if you have tears, prepare to shed them now
this was the most unkindest cut of all
I have seen some of the emails that were sent to Michael in recent months, largely coming from some young mathematicians, some postdocs in some somewhere: some of them bordering on what may well be called hate mail. I am afraid that what I got to see was probably just the tip of the iceberg: during our last conversation, just a few weeks before his death, Michael still complained about an incessant influx of such messages in his email, painful and distracting. Is this what we have become? Is this our new generation of reptiles devoid of all humanity, exclusively molded as non-sentient predators by the harshest academic Darwinian selection? What is especially tragic, beyond the fact itself, is that Michael was very much dependent in his well being on maintaining good relations to the young mathematicians. He loved his experience as a formal or informal mentor of students and collaborator with younger scholars. He was always a natural optimist at heart: even at times of personal difficulties he envisioned a brighter future ahead and the betterment of mathematics, as a discipline and a community.
ingratitude, more strong than traitors' arms,
quite vanquish'd him: then burst his mighty heart
I am also here looking straight at those of you who had known him for the longest time, the friends he once relied on: the ones who came and left, as fast as they could, when he called upon them for help some two or three years ago. I know you all, I don't forget, and I am here, looking at you. Because it was easier for you to be comforted in the self-reinforcement of your ageist prejudice, than to spend a moment of your precious time attempting to understand what was going on. It was especially the ones he had done his best to be supportive of, even in very recent times traveling very long distances when for his own sake he should not have, the same ones he complained about last time we spoke as being among the most aggressive against him in this latest run of time. (I am talking to you, Brutus: I know you so well, you were always so good at driving others to despair.) Why, all of you, why? What kind of rage or fear grips people's mind and turns them so inhuman when confronted with the fact that the making of mathematics is not a rosy garden of perfection but a thorny mess, and so is life?
they that have done this deed are honourable:
what private griefs they have, alas, I know not,
that made them do it: they are wise and honourable,
and will, no doubt, with reason answer you.
I come not, friends, to steal away your hearts.
I guess I was about the last who stayed. All of you who left failed to see that narrow mountain path winding through the rugged landscape, where some peaceful mathematical work could still take place, despite rapid alternation of gorges and peaks, despite the mounting roar of the outside storms. Perhaps it helped, or at least I'd like to think it did, even through small bits and pieces of unfinished work. It did help me, for sure: it was a joyous kind of work, unencumbered by the weight of expectation and prejudice. For quite some time I thought everything was going to be alright. It wasn't in the end, unfortunately though, believe me, not inevitably. It is too late right now to undo what has been done, but still I think the mathematical community as a whole should take a collective step back and do some soul searching and atonement over these events.
you are not wood, you are not stones, but men
The landscape of Scotland is harsh and beautiful at once. It is tragic in a Shakespearian sense. Our millennia of accumulated culture have primed us to associate great human achievement to the tragic in its most majestic form: the heroic and the tragic are one and the same thing in our still very Homeric worldview. Sir Michael Atiyah's life and achievements have had all the qualities of the classic Greek hero: from his reliance on an aesthetic idea of beauty in mathematics to the monumental scale of his work, to the final tragic standoff between his last mathematical dreams and the collective response of the community at large. The grand Shakespearian drama comes to an end, the curtain drops, and we are left alone on that empty stage wondering...
Here was a Caesar! When comes such another?
Images:
- Martin Creed, Work N.975 Everything is going to be alright, Scottish National Gallery, Edinburgh;
- Michael Atiyah's Collected Works, Oxford University Press;
- Alessando Piccolomini, De la sfera del mondo, 1540, Thomas Fisher Rare Book Library, University of Toronto;
- Marlon Brando, Julius Caesar, 1953;
- personal notebooks, 2017;
- Stob Bàn, Scottish Highlands, Getty Images.
Quotes are from recent public interviews of Sir Michael Atiyah and from Shakespeare's Julius Caesar, Act 3, Scene 2.